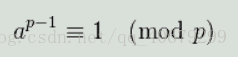0%

ACM模板

发表于 更新于 Valine：
本文字数： 20k 阅读时长 ≈ 34 分钟

一些比赛用的模板

数论

快速幂 O(logn)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 写法1：
ll mod_pow(ll x,ll n, ll mod){
    ll res=1;
    while(n>0){
        if(n&1)res=res*x%mod;
        x=x*x%mod;
        n>>=1;
    }
    return res;
}

//写法2:
ll mod_pow(ll x,ll n, ll mod){
    if(n==0) return 1;
    ll res=mod_pow(x*x%mod,n/2,mod);
    if(n&1) res=res*x%mod;
    return res;
}

矩阵快速幂

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
typedef long long ll;
typedef vector<int> vec;
typedef vector<vec> mat;
const int M=1e8+7;   //模的大小
//vector<int> a(10,1); //定义了10个整型元素的向量,且给出每个元素的初值为1
mat mul(mat &A,mat &B){
    mat C(A.size(),vec(B[0].size()));
    for(int i=0;i<A.size();i++){
        for(int k=0;k<B.size();k++){
            for(int j=0;j<B[0].size();j++){
                C[i][j]=(C[i][j]+A[i][k]*B[k][j])%M;
            }
        }
    }
    return C;
}
mat pow(mat A,ll n){
    mat B(A.size(),vec(A.size()));      // 输出矩阵
    for(int i=0;i<A.size();i++){
        B[i][i]=1;
    }
    while(n>0){
        if(n&1) B=mul(B,A);
        A=mul(A,A);
        n>>=1;
    }
    return B;
}

GCD 欧几里得算法 O（log max(a,b)）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int gcd(int a,int b){
    if(b==0) return a;
    return gcd(b,a%b);
}

F(x)是斐波那契数列
GCD(F[n],F[m])=F[gcd(n,m)

//扩展欧几里得算法  ax+by=gcd(a,b);
    int extgcd(int a,int b,int& x,int& y){
        int d=a;
        if(b!=0){
            d=extgcd(b,a%b,y,x);
            y-=(a/b)*x;
        }
        else{
            x=1;
            y=0;
        }
        return d;
    }

素数筛表

时间复杂度接近O(n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
int vis[MAXN];
int prime[MAXN];
void Prime()
{
    int cnt=0;
    for(int i=2;i<=n;i++)
    {
        if(!vis[i]) prime[cnt++]=i;
        for(int j=0;j<cnt&&i*prime[j]<=n;j++)
        {
            vis[i*prime[j]]=i;
            if(i%prime[j]==0) break;
        }
    }
}

二次探测定理：

奇素数p（即除2外的素数）
$xmodp^2=1$的解只有x=1和x=p-1

素数定理：

随着x的增长,$π(x)/(x/ln(x))=1$，(π(x)为小于x的素数的个数)

递推式转矩阵

费马小定理和欧拉公式

费马小定理(Fermat’s little theorem)是数论中的一个重要定理，在1636年提出。如果p是一个质数，而整数a不是p的倍数，则有$a^{p-1}≡1(mod p)$。

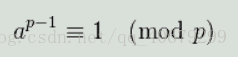
费马小定理：$2^nmodm=2^{nmod(m-1）}mod~~m$ （这个怎么推我还不知道）

在数论中，欧拉定理,（也称费马-欧拉定理）是一个关于同余的性质。欧拉定理表明，若n,a为正整数，且n,a互质，则: $a^{φ(n)}≡1(mod n)$
φ(n)为欧拉函数，定义为不超过n的整数中与n互素的个数。
欧拉降幂公式： $a^b≡a^{bmodφ(n)+φ(n)}mod n$

1
2
3
4
5
6
7
8
9
10
11
12
// 求欧拉函数值.
int euler_phi(int n){
    int res=n;
    for(int i=2;i*i<=n;i++){
        if(n%i==0){
            res=res/i*(i-1);
            for(;n%i==0;n/=i);
        }
    }
    if(n!=1) res=res/n*(n-1);
    return res;
}

卢卡斯定理

Lucas定理是用来求 c(n,m) mod p，p为素数的值。
表达式：C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p
Lucas定理：我们令n=sp+q , m=tp+r .（q ，r ≤p）
那么:

</div>

1
2


BBP公式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
#include <iostream>
#define MAX_C 56000
int a = 10000, b, c = MAX_C, d, e, f[MAX_C + 1], g, n, ans, cnt;
using namespace std;
/*
* BBP公式   参照CCDN的姬小野博客   本人还不会....
*/
int main() {
    while(~scanf("%d", &n)){
    for (; b - c; )
        f[b++] = a / 5;
    for (; d = 0, g = c * 2;
         c -= 14, ans = e + d / a, e = d % a, cnt++)
    { if (cnt * 4 > n) break;
     for (b = c; d += f[b]*a, f[b] = d % --g, d /= g--, --b; d *= b); }
    if (n % 4 == 0) cout << (ans / 1000);
    else if (n % 4 == 1) cout << ((ans / 100) % 10);
    else if (n % 4 == 2) cout << ((ans / 10) % 10);
    else if (n % 4 == 3) cout << (ans % 10);
    printf("\n");}
    return 0;
}

图论

最短路问题

任意两点间的最短路问题(Floyd算法)

1
2
3
4
5
6
7
8
9
10
11
int d[MAX_v][MAX_V]  //无法到达时，权值为INF，主对角线为0
int V   // 顶点数
void Floyd(){
    for(int k=0;k<V;k++){
        for(int i=0;i<V;i++){
            for(int j=0;j<V;j++){
                d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
            }
        }
    }
}

单源最短路问题(Dijkstra算法)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
int cost[MAX_V][MAX_V];     //图的临接矩阵
int d[MAX_V];               //顶点s（起点）到各点的最短距离
bool used[MAX_V];           //是否已经访问过
int V;                      //顶点数
int prev[MAX_V];            //前趋顶点 （路径还原）

void Dijkstra(int s){
    fill(d,d+v,INF);
    fill(used,used+V,false);
    fill(prev,prev+V,-1);
    d[s]=0;
    while(true){
        int v=-1;
        for(int u=0;u<V;u++){
            if(!used[u]&&(v==-1||d[u]<d[v])) v=u;
        }
        if(v==-1) break;
        used[v]=true;
        for(int u=0;u<V;u++){
            if(d[u]>d[v]+cost[v][u]){
                d[u]=d[v]+cost[v][u];
                prev[u]=v;
            }
        }
    }
}

//到顶点t的最短路
vector<int> get_path(int t){
    vector<int> path;
    for(;t!=-1;t=prev[t]) path.push_back(t);
    reverse(path.begin(),path.end());
    return path;
}

最小生成树

Prim算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int cost[MAX_V][MAX_V];         //临接矩阵表示边
int mincost[MAX_V];             //从集合X出发的边到每个顶点的最小权值
bool used[MAX_V];               //顶点i是否包含在集合X中
int V;                          //顶点数

int prim(){
    for(int i=0;i<V;i++){
        mincost[i]=INF;
        used[i]=false;
    }
    mincost[0]=0;
    int res=0;
    while(true){
        int v=-1;
        for(int u=0;u<V;u++){
            if(!used[u]&&(v==-1||mincost[u]<mincost[v])) v=u;
        }
        if(v==-1) break;
        used[v]=true;                //把顶点v加入X
        res+=mincost[v];             //把边的长度加到结果里
        for(int u=0;u<V;u++){
            mincost[u]=min(mincost[u],cost[v][u]);
        }
    }
    return res;
}

Kruskal算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
struct edge{
    int u,v,cost;
};
bool comp(const edge& e1,const edge& e2){
    return e1.cost < e2.cost;
}

int par[MAX_N]   //父亲
int rank[MAX_N]     //数的高度

void init_union_find(int n){
    for(int i=0;i<n;i++){
        par[i]=i;
        rank[i]=0;
    }
}

int find(int x){
    if(par[x]==x){
        return x;
    }else{
        return par[x]=find(par[x]);
    }
}

void unite(int x,int y){
    x=find(x);
    y=find(y);
    if(x==y) return;
    if(rank[x]<rank[y]){
        par[x]=y;
    }else{
        par[y]=x;
        if(rank[x]==rank[y])rank[x]++;
    }
}


edge es[MAX_E];
int V,E;            //顶点数和边数
int kruskal(){
    sort(es,es+E,comp);     //将边排序
    init_union_find(V);     //并查集初始化
    int res=0;
    for(int i=0;i<E;i++){
        edge e=es[i];
        if(!same(e.u,e.v)){
            unite(e.u,e.v);
            res+=e.cost;
        }
    }
    return res;
}

最大流最小割问题

摘自：https://blog.csdn.net/yo_bc/article/details/72825629

FORD-FULKERSON(FF)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <algorithm>
#include <iostream>
#include <string.h>
#include <cstdio>
#include <stack>
using namespace std;
const int inf = 0x7fffffff;
const int maxn = 205;
struct node
{
	int v, w, next;
}edge[maxn*maxn];
int no, n, m;
int head[maxn], pre[maxn], rec[maxn], flow[maxn];
stack<int> stk;
void init()
{
	no = 0;
	memset(head, -1, sizeof head);
}
//静态邻接表存边 
void add(int u, int v, int w)
{
	edge[no].v = v; edge[no].w = w;
	edge[no].next = head[u]; head[u] = no++;
	edge[no].v = u; edge[no].w = 0;
	edge[no].next = head[v]; head[v] = no++;
}
int dfs(int S, int T)
{
	memset(pre, -1, sizeof pre);
	while(!stk.empty()) stk.pop();
	pre[S] = S; flow[S] = inf;
	stk.push(S);
	while(!stk.empty())	//用栈迭代替代dfs深搜 
	{
		int top = stk.top(); stk.pop();
		int k = head[top];
		while(k != -1)
		{
			if(pre[edge[k].v] == -1 && edge[k].w > 0)
			{
				flow[edge[k].v] = min(flow[top], edge[k].w);
				pre[edge[k].v] = top;
				rec[edge[k].v] = k;
				stk.push(edge[k].v);
			}
			k = edge[k].next;
		}
		if(pre[T] != -1) return flow[T];
	}
	return -1;
}
int FF(int s, int t)
{
	int ans = 0, add;
	while((add = dfs(s, t)) != -1)	//直到找不到增广路 
	{
		ans += add;
		int k = t;
		while(k != s)
		{
			edge[rec[k]].w -= add;
			edge[rec[k]^1].w += add;
			k = pre[k];
		}
	}
	return ans;
}
int main()
{
	ios::sync_with_stdio(0);
	int u, v, w;
	while(cin >> m >> n) 
	{
		init();
		for(int i = 0; i < m; ++i)
		{
			cin >> u >> v >> w;
			add(u, v, w); 
		}
		cout << FF(1, n) << endl;
	}
	return 0;
}

Edmonds-Karp(EK)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <algorithm>
#include <iostream>
#include <string.h>
#include <cstdio>
#include <queue>
using namespace std;
const int inf = 0x7fffffff;
const int maxn = 205;
struct node
{
	int v, w, next;
}edge[maxn*maxn];
int no, n, m;
int head[maxn], pre[maxn], rec[maxn], flow[maxn];
queue<int> q;
void init()
{
	no = 0;
	memset(head, -1, sizeof head);
}
//静态邻接表存边 
void add(int u, int v, int w)
{
	edge[no].v = v; edge[no].w = w;
	edge[no].next = head[u]; head[u] = no++;
	edge[no].v = u; edge[no].w = 0;
	edge[no].next = head[v]; head[v] = no++;
}
int dfs(int S, int T)
{
	memset(pre, -1, sizeof pre);
	while(!q.empty()) q.pop();
	pre[S] = S; flow[S] = inf;
	q.push(S);
	while(!q.empty())	
	{
		int top = q.front(); q.pop();
		int k = head[top];
		while(k != -1)
		{
			if(pre[edge[k].v] == -1 && edge[k].w > 0)
			{
				flow[edge[k].v] = min(flow[top], edge[k].w);
				pre[edge[k].v] = top;
				rec[edge[k].v] = k;
				q.push(edge[k].v);
			}
			k = edge[k].next;
		}
		if(pre[T] != -1) return flow[T];
	}
	return -1;
}
int EK(int s, int t)
{
	int ans = 0, add;
	while((add = dfs(s, t)) != -1)	//直到找不到增广路 
	{
		ans += add;
		int k = t;
		while(k != s)
		{
			edge[rec[k]].w -= add;
			edge[rec[k]^1].w += add;
			k = pre[k];
		}
	}
	return ans;
}
int main()
{
	ios::sync_with_stdio(0);
	int u, v, w;
	while(cin >> m >> n) 
	{
		init();
		for(int i = 0; i < m; ++i)
		{
			cin >> u >> v >> w;
			add(u, v, w); 
		}
		cout << EK(1, n) << endl;
	}
	return 0;
}

Dinic

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
#include <algorithm>
#include <iostream>
#include <string.h>
#include <cstdio>
#include <queue>
using namespace std;
const int inf = 0x7fffffff;
const int maxn = 205;
struct node
{
	int v, w, next;
}edge[maxn*maxn];
int dis[maxn], pre[maxn], rec[maxn], head[maxn], block[maxn];
int n, m, no;
queue<int> q;
//静态邻接表存边 
inline void add(int u, int v, int w)
{
	edge[no].v = v; edge[no].w = w;
	edge[no].next = head[u]; head[u] = no++;
	edge[no].v = u; edge[no].w = 0;
	edge[no].next = head[v]; head[v] = no++;
}
inline void pre_init()
{
	no = 0;
	memset(head, -1, sizeof head);
}
void init(int S, int T)
{	//初始化一定要注意把所涉及的都覆盖到 
	for(int i = 0; i <= n; ++i)
	{ 
		dis[i] = inf;
		block[i] = 0;	//标记阻塞点 
	} 
	while(!q.empty()) q.pop();
	dis[S] = 0; q.push(S);
	while(!q.empty())	//生成层次图 
	{
		int tp = q.front(); q.pop();
		int k = head[tp];
		while(k != -1)
		{
			if(dis[edge[k].v] == inf && edge[k].w)
			{
				dis[edge[k].v] = dis[tp] + 1;
				q.push(edge[k].v);
			}
			k = edge[k].next;
		}
	}
}
int dinic(int S, int T)
{
	int top = S, ans = 0, flow = inf;
	pre[S] = S; init(S, T);
	while(dis[T] != inf)	//当S无法到达T，不能再增广了 
	{
		int k = head[top];
		while(k != -1)
		{
			if(edge[k].w && dis[edge[k].v] == dis[top]+1 
			&& !block[edge[k].v]) break;
			k = edge[k].next;
		}
		if(k != -1)	//找到下一节点 
		{
			int v = edge[k].v;
			flow = min(flow, edge[k].w);
			pre[v] = top; rec[v] = k;
			top = v;
			if(top == T)
			{
				ans += flow;
				v = -1; k = T;
				while(k != S)
				{
					edge[rec[k]].w -= flow;
					edge[rec[k]^1].w += flow;
					if(!edge[rec[k]].w) v = k;	//寻找距S最近的一个"瓶颈"边 
					k = pre[k];
				}
				flow = inf;	//此处flow必须在外面，大佬的板子可能没注意到，我认为是必须的 
				if(v != -1)	//找到"瓶颈"边 
				{
					top = pre[v];
					k = top;
					while(k != S)
					{
						flow = min(edge[rec[k]].w, flow);
						k = pre[k];
					}
				}
			}
		}
		else
		{
			block[top] = 1;	//找不到下一节点成为阻塞点 
			top = pre[top];	//回溯 
			if(block[S]) init(S, T);//如果S被阻塞，重新计算层次图
			//阻塞点的产生也造成了flow的最小值可能是后面的值，虽然进行一次
			//增广并没什么问题，但上述寻找瓶颈边的判断则是必须的了。 
		}
	}
	return ans;
}
int main()
{
	ios::sync_with_stdio(0);
	int u, v, w;
	while(cin >> m >> n)
	{
		pre_init();
		for(int i = 1; i <= m; ++i)
		{
			cin >> u >> v >> w;
			add(u, v, w);
		}
		cout << dinic(1, n) << endl;
	}
	return 0;
}
 
 
/**********************比赛版本***********************/
 
#include <algorithm>
#include <iostream>
#include <string.h>
#include <cstdio>
#include <queue>
using namespace std;
const int inf = 0x3f3f3f3f;
const int maxn = 205;
const int maxm = maxn*maxn;
struct node{int w; int v, next;} edge[maxm];
int pre[maxn], rec[maxn], head[maxn], block[maxn];
int dis[maxn];
int n, m, no;
int S, T;
queue<int> q;
inline void init()
{
	no = 0;
	memset(head, -1, sizeof head);
}
inline void add(int u, int v, int w)
{
	edge[no].v = v; edge[no].w = w;
	edge[no].next = head[u]; head[u] = no++;
	edge[no].v = u; edge[no].w = 0;
	edge[no].next = head[v]; head[v] = no++;
}
void reset(int S, int T)
{
	memset(dis, 0x3f, sizeof dis);
	memset(block, 0, sizeof block);
	q.push(S); dis[S] = 0;
	while(!q.empty())
	{
		int top = q.front(); q.pop();
		for(int k = head[top]; k != -1; k = edge[k].next)
		if(dis[edge[k].v] == inf && edge[k].w)
			dis[edge[k].v] = dis[top]+1, q.push(edge[k].v);
	}
}
int dinic(int S, int T)
{
	int ans = 0, flow = inf;
	int top = S;
	reset(S, T); pre[S] = S;
	while(dis[T] != inf)
	{
		int k, tmp;
		for(k = head[top]; k != -1; k = edge[k].next)
		{
			if(edge[k].w && dis[edge[k].v]==dis[top]+1 && 
			!block[edge[k].v]) break;
		}
		if(k != -1)
		{
			tmp = edge[k].v;
			flow = min(flow, edge[k].w);
			pre[tmp] = top, rec[tmp] = k;
			top = tmp;
			if(top == T)
			{
				ans += flow; tmp = -1;
				for(; top != S; top = pre[top])
				{
					edge[rec[top]].w -= flow;
					edge[rec[top]^1].w += flow;
					if(!edge[rec[top]].w) tmp = top;
				}
				flow = inf;
				if(tmp != -1)
				{
					top = pre[tmp];
					for(; top != S; top = pre[top])
					flow = min(flow, edge[rec[top]].w);
					top = pre[tmp];
				}
			}
		}
		else
		{
			block[top] = 1;
			top = pre[top];
			if(block[S]) reset(S, T);
		}
	}
	return ans;
}
void mapping()
{
	int u, v, w;
	for(int i = 1; i <= m; ++i)
	{
		scanf("%d %d %d", &u, &v, &w);
		add(u, v, w);
	}
}
int main()
{
	while(~scanf("%d %d", &m, &n))
	{
		S = 1, T = n;
		init();
		mapping();
		printf("%d\n", dinic(S, T));
	}
	return 0;
}

Shortest Augmenting Paths(SAP

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
#include <algorithm>  
#include <iostream>  
#include <string.h>  
#include <cstdio>  
#include <queue>  
using namespace std;  
const int inf = 0x7fffffff;  
const int maxn = 205;  
const int maxm = maxn*maxn; //一定要好好计算边的数量   
struct node  
{  
    int v, w, next;  
}edge[maxm];  
int dis[maxn], pre[maxn], rec[maxn], head[maxn], gap[maxn], now[maxn];  
int n, m, no, up;  //up指逆层次图可能还有增广路时dis的上界 
queue<int> q;  
//静态邻接表存边   
inline void add(int u, int v, int w)  
{  
    edge[no].v = v; edge[no].w = w;  
    edge[no].next = head[u]; head[u] = no++;  
    edge[no].v = u; edge[no].w = 0;  
    edge[no].next = head[v]; head[v] = no++;  
}  
inline void pre_init()  
{  
    no = 0;  up = n;
    memset(head, -1, sizeof head);  
}  
void init(int S, int T)  
{
    for(int i = 0; i <= up; ++i)   
    {
    	now[i] = head[i];   //now用作当前弧的优化   
    	//注意这里now数组要把所有用到的标号都存过来  
    	gap[i] = 0, dis[i] = inf;
    	//初始化一定要注意把所涉及的都覆盖到   
	}
    while(!q.empty()) q.pop();  
    dis[T] = 0; q.push(T);  
    while(!q.empty())   //生成逆层次图   
    {  
        int tp = q.front(); q.pop();  
        ++gap[dis[tp]];  
        int k = head[tp];  
        while(k != -1)  
        {  
            if(dis[edge[k].v] == inf && edge[k^1].w)  
            {  
                dis[edge[k].v] = dis[tp]+1;  
                q.push(edge[k].v);  
            }  
            k = edge[k].next;  
        }  
    }  
}  
int SAP(int S, int T)  
{  
    int ans = 0, flow = inf, top = S;  
    pre[S] = S; init(S, T);  
    while(dis[S] < up)    //当S到T的距离大于等于点的个数时肯定就不能再增广了   
    {                   //切记此处与节点数比较，因为通过方向变会造成距离可能达到节点数  
        if(top == T)  
        {  
            ans += flow;  
            while(top != S) //修改残留网络，并置top为S   
            {  
                edge[rec[top]].w -= flow;  
                edge[rec[top]^1].w += flow;  
                top = pre[top];  
            }  
            flow = inf;  
        }  
        int k = now[top];  
        while(k != -1)  
        {  
            int v = edge[k].v;  
            if(edge[k].w && dis[top] == dis[v]+1)  
            {  
                flow = min(flow, edge[k].w);  
                pre[v] = top; rec[v] = k;  
                now[top] = k;//当前弧的优化   
                top = v;  
                break;  
            }  
            k = edge[k].next;  
        }  
        if(k == -1)  
        {  
            int mind = n;  
            if(--gap[dis[top]] == 0) break;//出现断层，间隙优化   
            int k = now[top] = head[top];//改变当前点的距离标号，也要清除之前的当前弧优化的影响   
            while(k != -1)  
            {  
                if(edge[k].w && mind>dis[edge[k].v]) mind = dis[edge[k].v];  
                k = edge[k].next;  
            }  
            ++gap[dis[top] = mind+1];  
            top = pre[top];//回溯到上一个点   
        }  
    }  
    return ans;  
}
int main()  
{
    ios::sync_with_stdio(0);
	int u, v, w;
	while(cin >> m >> n)
	{
		pre_init();
		for(int i = 1; i <= m; ++i)
		{
			cin >> u >> v >> w;
			add(u, v, w);
		}
		cout << SAP(1, n) << endl;
	}
    return 0;  
}
 
 
/**********************比赛版本***********************/
 
#include <algorithm>  
#include <iostream>  
#include <string.h>  
#include <cstdio>  
#include <queue>  
using namespace std;  
const int inf = 0x3f3f3f3f;  
const int maxn = 205;  
const int maxm = maxn*maxn;
struct node{int w; int v, next;} edge[maxm];  
int pre[maxn], rec[maxn], head[maxn], gap[maxn], now[maxn];  
int dis[maxn];
int n, m, no, up;  
int S, T; 
queue<int> q;
inline void add(int u, int v, int w)  
{  
    edge[no].v = v; edge[no].w = w;  
    edge[no].next = head[u]; head[u] = no++;  
    edge[no].v = u; edge[no].w = 0;  
    edge[no].next = head[v]; head[v] = no++;  
}  
inline void pre_init()  
{  
    no = 0;
    memset(head, -1, sizeof head);  
}  
void init(int S, int T)  
{  
    memset(gap, 0, sizeof gap);  
    memset(dis, 0x3f, sizeof dis);  
    for(int i = 0; i <= up; ++i)   
    now[i] = head[i];
    while(!q.empty()) q.pop();  
    dis[T] = 0; q.push(T);  
    while(!q.empty()) 
    {  
        int tp = q.front(); q.pop();  
        ++gap[dis[tp]];  
        int k = head[tp];  
        while(k != -1)  
        {  
            if(dis[edge[k].v] == inf && edge[k^1].w)  
            {  
                dis[edge[k].v] = dis[tp]+1;  
                q.push(edge[k].v);  
            }  
            k = edge[k].next;  
        }  
    }  
}  
int SAP(int S, int T)  
{
    int ans = 0, flow = inf;
	int top = S;  
    pre[S] = S; init(S, T);  
    while(dis[S] < up)
    {
        if(top == T)  
        {  
            ans += flow;  
            while(top != S)
            {  
                edge[rec[top]].w -= flow;  
                edge[rec[top]^1].w += flow;  
                top = pre[top];  
            }  
            flow = inf;  
        }  
        int k = now[top];  
        while(k != -1)  
        {  
            int v = edge[k].v;  
            if(edge[k].w && dis[top] == dis[v]+1)  
            {  
                flow = min(flow, edge[k].w);  
                pre[v] = top; rec[v] = k;  
                now[top] = k; top = v;  
                break;  
            }  
            k = edge[k].next;  
        }  
        if(k == -1)  
        {  
            int mind = up;  
            if(--gap[dis[top]] == 0) break;
            int k = now[top] = head[top];
            while(k != -1)  
            {  
                if(edge[k].w && mind>dis[edge[k].v]) mind = dis[edge[k].v];  
                k = edge[k].next;  
            }  
            ++gap[dis[top] = mind+1];  
            top = pre[top];  
        }  
    }  
    return ans;  
}  
void mapping()
{
	int u, v, w;
	for(int i = 1; i <= m; ++i)  
    {  
        scanf("%d %d %d", &u, &v, &w); 
        add(u, v, w);  
    }
}
int main()  
{
    while(~scanf("%d %d", &m, &n))  
    {  
		up = n, S = 1, T = n;
        pre_init();  
        mapping();
        printf("%d\n", SAP(S, T)); 
    }  
    return 0;  
}

二分图

匈牙利算法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
bool CP[MAX][MAX];           //cp[i][j]=1 表示i能和j组cp
bool used[MAX];             //记录是否已经被访问
int linked[MAX];            //linked[i]=j 表示i和j组cp

bool fun(int x){
	int i
	for (i=1;i<=N;i++){    
		if (CP[x][i]==true && used[i]==false)      
		{
			used[i]=1;
			if (linked[i]==0 || fun(linked[i])) { 
				linked[j]=x;
				return true;
			}
		}
	}
	return false;
}
int hungary(){
	int ans=0;
	memset(linked,0,sizeof(linked));
	for(int i=1;i<=M;i++){
	       memset(used,0,sizeof(used));				
	       if(fun(i)) 
	           ans++;
	   }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
// 转载： https://blog.csdn.net/qq_32265245/article/details/53046750
/*
    |求解最大匹配问题|
    |dfs实现|
*/

int v1, v2;  
bool Map[501][501];  
bool visit[501];  
int link[501];  
int result;  

bool dfs(int x)  {  
    for (int y = 1; y <= v2; ++y)  {  
        if (Map[x][y] && !visit[y])  {  
            visit[y] = true;  
            if (link[y] == 0 || dfs(link[y]))  {  
                link[y] = x;  
                return true;  
            } } }  
    return false;  
}  


void Search()  {  
    for (int x = 1; x <= v1; x++)  {  
        memset(visit,false,sizeof(visit));  
        if (dfs(x))  
            result++;  
    }
}

博弈

巴仕博弈（Bash Game）

描述：
只有一堆n个物品，两个人轮流从这堆物品中取物，规定每次至少取一个，最多取m个。最后取光者得胜。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<bits/stdc++.h>
using namespace std;
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        int n,m;
        cin>>n>>m;
        if(n%(m+1))
            cout<<"first"<<endl;
        else 
            cout<<"second"<<endl;
    }
    return 0;
}

威佐夫博弈（Wythoff Game）

描述：有两堆各若干个物品，两个人轮流从某一堆或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜
1，我们用（a[k]，b[k]）（a[k] ≤ b[k] ,k=0，1，2，…,n)表示两堆物品的数量并称其为局势。

2，如果甲面对（0，0），那么甲已经输了，这种局势我们称为奇异局势。

3，奇异局（举例）

首先列举人们已经发现的前几个奇异局势：（0，0）、（1，2）、（3，5）、（4，7）、（6，10）

（8，13）、（9，15）、（11，18）、（12，20）。

通过观察发现：a[0]=b[0]=0,a[k]是未在前面出现过的最小自然数,而 b[k]= a[k] + k。

4，奇异局势有如下三条性质：

1）任何自然数都包含且仅包含在一个奇异局势中。

2）任意操作都可以使奇异局势变为非奇异局势。

3）必有一种操作可以使非奇异局势变为奇异局势。

5，奇异局势公式：

a[k]=[k*(1+√5)/2]，b[k]=a[k]+k。

(k=0,1,2……，[ ]表示取整）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//威佐夫博弈模板
#include<bits/stdc++.h>
using namespace std;
const double Gsr=(1+sqrt(5.0))/2;
int main()
{
    int a,b;
    while(~scanf("%d%d",&a,&b))
    {
        if(a>b)
            swap(a,b);
        if(a == (int)(Gsr*(b-a))) //奇异局势，先拿者输
            puts("First Lose");
        else
            puts("First Win");
    }
    return 0;
}

Nim博弈

描述：有n堆石子，每堆各有$a_i$课石子。Alice和Bob轮流从非空的石子堆中取走至少一颗石子。
Alice先取，取光所有石子的一方获胜。当双方都采取最优策略时，谁会获胜？

结论：计算所有$a_i$的异或值，如果非零则先手胜，为零则后手胜。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
//Nim模板
#include<bits/stdc++.h>
using namespace std;
const double Gsr=(1+sqrt(5.0))/2;
int N，A[MAX_N];
int main()
{
    cin>>N;
    for(int i=0;i<N;i++) cin>>A[i];
    int x=0;
    for(int i=0;i<N;i++) x^=A[i];
    if(x!=0) 
        puts("Alice");
    else 
        puts("Bob");
    return 0;
}

SG函数

描述：Alice和Bob在玩这样一个游戏。给定k个数字$a_1,a_2,···,a_k$。一开始，有n堆硬币，每堆各有$x_i$枚硬币。Alice和Bob轮流选出一堆硬币，从中取出一些硬币。每次所取硬币的枚数一定要在$a_1,a_2,···,a_k$当中。Alice先取，取光硬币的一方获胜。当双方都采取最优策略时，谁会获胜？

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
//SG函数模板
int N,K,X[MAX_N]，A[MAX_K];
//利用动态规划计算grundy值的数组
int grundy[MAX_X+1];
void solve(){
    //轮到自己时为0则必败
    grundy[0]=0;
    //计算grundy值
    int max_x=*max_element(X,X+N);
    for(int j=1;j<=max_x;j++){
        set<int> s;
        for(int i=0;i<K;i++){
            if(A[i]<=j) s.insert(grundy[j-A[i]]);
        }
        int g=0;
        while(s.count(g)!=0)g++;
        grundy[j]=g;
    } 
    //判断胜负
    int x=0;
    for(int i=0;i<N;i++) x^=grundy[X[i]];
    if(x!=0) puts("Alice");
    else puts("Bob");
}

-------------本文结束感谢您的阅读-------------